Fuentes de datos
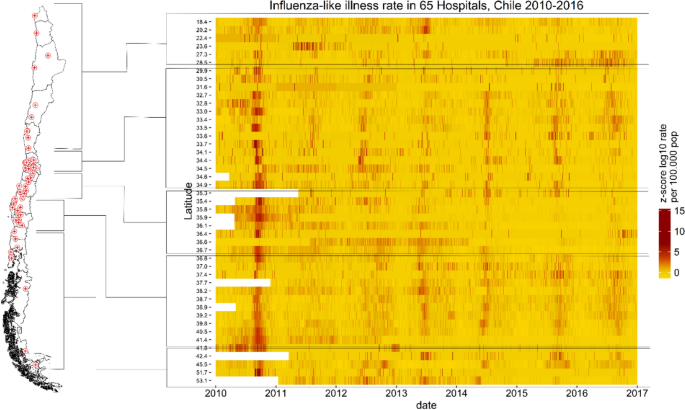
Obtuvimos datos diarios de casos de ILI recopilados por el Ministerio de Salud de Chile entre 2010 y 2016 en los departamentos de emergencia de hospitales públicos. ILI es una medida aceptable que se correlaciona con el seguimiento de laboratorio de las tendencias poblacionales.21. Utilizamos datos de vigilancia de ILI de los departamentos de emergencia en lugar de laboratorios centinela, dado que la vigilancia de la influenza se limita a 25 hospitales en todo el país con una cobertura territorial limitada. Complementamos los datos de población cuadriculados de WorldPop con datos oficiales del gobierno sobre ubicaciones de hospitales, información del censo y cobertura de población para estimar la población con acceso a cada hospital.25,26,27.28.
Excluimos los hospitales comunitarios, los hospitales sin departamentos de emergencia y los hospitales que informaron <75 % de los datos diarios de los departamentos de emergencia entre 2011 y 2016 (<1920 días). También se excluyeron los hospitales a los que les faltaban ≥5% de datos en grupos de 20 días consecutivos para reducir los errores de imputación. Supusimos que los datos faltantes se debían al azar. Se probaron doce métodos de imputación diferentes utilizando datos faltantes generados aleatoriamente a partir de los datos originales. La imputación de series de tiempo con suavizado de Kalman mostró los mejores resultados para estimar la estacionalidad en comparación con los datos originales.29.30.
Preparación de datos
Dado que el acceso a los departamentos de emergencia disminuye al aumentar la distancia, elegimos un radio de cinco kilómetros para estimar la población cubierta por cada hospital.31.32. Obtuvimos estimaciones de población de cuadrícula de 100 × 100 m de WorldPop para 2010 y 2015 y las ajustamos según los datos del censo para cada municipio y año.28. Utilizamos interpolación lineal para imputar estimaciones de población para 2011-2014 y 2016. Para cada área de cobertura hospitalaria, ajustamos la proporción de personas con seguro público para cada municipio por año y calculamos las tasas diarias de ILI en la población estimada.26. Los datos de hospitales de la misma red de salud y ubicados a menos de 5 km entre sí se combinaron en una única serie temporal. Para determinar la estacionalidad en las redes de salud, calculamos la tasa de ILI por red sumando los datos de ILI y de población de todos los hospitales de cada red de salud. Utilizamos una posición mediana de los hospitales en cada red para determinar la latitud de la red de salud.
Transformar datos usando wavelets
Utilizamos el análisis wavelet para determinar la mejor periodicidad (por ejemplo, estacionalidad) de la influenza en 29 redes de salud chilenas. La transformada wavelet es un método adecuado para determinar la estacionalidad de series temporales no estacionarias y para determinar la estacionalidad de una serie temporal periódica sin asumir a priori una estacionalidad específica.33. La transformada wavelet es la correlación cruzada de series temporales de tasas de ILI con wavelets de diferentes “anchos” o “escalas” a lo largo del tiempo.33. La onda de Morlet se ha utilizado para calcular tasas de enfermedades infecciosas como el dengue, la tos ferina, el sarampión y la gripe.34,35,36,37,38.39. Calculamos la transformada wavelet de Morlet para todo el país, cada red de salud y cada hospital individual.34,35,40.
Realizamos transformaciones wavelet para períodos (escalas) que van de 14 a 144 semanas. La significancia estadística se probó comparando la señal de onda con 1000 series temporales generadas aleatoriamente (es decir, ruido blanco) con un nivel de significancia de 0,05.41. El espectro de potencia de wavelets local se utilizó para visualizar la correlación cruzada entre las tasas y cada grupo de wavelets (Fig. 2b, S1 y ecuación s1).33,42.
Para determinar la mejor estacionalidad (períodos de mayor potencia), calculamos la potencia promedio para cada período, en todos los puntos de tiempo, a partir del espectro de potencia wavelet local para Chile, cada red de salud y para hospitales individuales, según el trabajo de Torrence.42:
$$ \overline{W}^{2} \left( s \right) = \frac{1}{N} \mathop \sum \limits_{n = 0}^{N} \left| {Wn\left( s \right)} \right|^{2} $$
(3)
O norte representa el número de observaciones.
Definimos la mejor estacionalidad de la influenza como la extensión de los períodos que caen dentro del percentil 95 de la potencia media de un período a otro.
Asociación entre el momento de la epidemia y la latitud de la red de salud
Para determinar la asociación entre el momento de la gripe y la latitud, seleccionamos la transformada wavelet utilizando el rango correspondiente a la mejor estacionalidad para cada red de salud. Reconstruimos los ciclos epidémicos utilizando el filtro definido por Torrence y Campo (S1 y Ecuación s2).42. Para cada red de salud, la fecha de inicio de una epidemia anual de ILI se definió como la fecha en la que los ciclos reconstruidos alcanzaron el punto medio entre el punto más bajo y el pico de la señal para cada año de 2010 a 2016. Calculamos el día pico para el período correspondiente, así como las fechas medianas de inicio y pico de cada red de salud.
Desarrollamos modelos de regresión lineal univariados, por partes y multivariados para evaluar la relación entre el predictor, la latitud y los resultados del inicio y pico del brote en las redes de salud. Para los modelos por partes, separamos el país en tres zonas: norte, centro y sur con latitudes del sur. < 31, 31-40 et > 41, respectivamente. Para el análisis multivariado incluimos latitud y población como variables continuas, una variable binaria para describir la presencia de un aeropuerto en el territorio de la red de salud y variables ficticias para los años 2010 a 2016 con 2013 como referencia. La cepa de influenza predominante se excluyó debido a dependencias lineales con los años 2011 y 2014. El modelo multivariado final se seleccionó probando todas las combinaciones de predictores posibles con el método de regresión de suma de cuadrados y comparando BIC y Mallow Cp.43.
Olas itinerantes locales de influenza
Una wavelet de Morlet es una función compleja que comprende una parte real y una parte imaginaria. La parte real permite la separación de la amplitud y la extracción de la fase de una señal así como la temporización en un periodo concreto, independientemente de la amplitud.33,42,44. Las fases son ciclos continuos presentados como ángulos de fase en radianes de -π a +π41. Extrajimos los ángulos de fase utilizando una banda de períodos dentro del percentil de potencia 95, como lo describió anteriormente Torrence (S1 y Ec. 3).
Para definir una onda viajera local, utilizamos un modelo de regresión polinómica local de segundo grado (LOESS) con correlación de Spearman entre pares de series temporales de ángulo de fase de la red de salud versus distancia al parámetro α = 0,75. A continuación, determinamos que la distancia correspondía a la correlación más pequeña después de que se descubrió un segmento lineal inicial del modelo LOESS. Todos los pares de redes de salud dentro de este límite de distancia se incluyeron para cada uno de los 29 modelos de ondas viajeras lineales.
Calculamos la diferencia mediana de la serie temporal del ángulo de fase (sincronización) para todos los pares posibles de redes de salud y probamos la asociación con la distancia. El signo de la diferencia de fase representó la sincronización relativa del SG. Una diferencia negativa indicó un retraso en el momento de aparición de la influenza (entrante); una diferencia positiva indicó ondas viajeras salientes. Ajustamos dos modelos lineales para cada red de salud a todas las demás, uno para diferencias de fase positivas y el segundo para diferencias de fase negativas:
$$ \theta _{{p,q}} = \left\{ {\begin{array}{*{20}c} {C – \beta _{p} d_{{p,q}} \quad para \quad \theta < 0,\quad entrant\;waves} \\ {C + \beta _{p} d_{{p,q}} \quad pour \quad \theta > 0, \quad out\;ondas} \\ \end{array} } \right\} $$
(4)
O θp, q esta es la brecha entre las redes de salud pag Y q Y dpqq es la distancia en kilómetros entre las redes de salud. El signo de distancia se ha invertido para tiempos de retraso negativos para una visualización más intuitiva de las ondas entrantes. Consideramos una onda viajera local como una asociación lineal significativa entre la diferencia de fase y la distancia utilizando un nivel de significancia de Bonferroni corregido de 0,0017.
Desarrollamos modelos de regresión logística separados para ondas entrantes y salientes para determinar la asociación entre ondas progresivas y estimaciones de población, ajustando para cada latitud de la red de salud. Para evaluar la discriminación del modelo, utilizamos la curva característica operativa del receptor y el área bajo la curva (AUC).45.
Utilizamos el paquete R versión 3.6.2 Leaps para la selección del modelo y el paquete R WaveletComp para la transformada wavelet y la extracción de fase.46,47.
Presentaciones anteriores
Este trabajo no ha sido presentado ni publicado anteriormente.

“Practicante de la cultura pop de toda la vida. Creador. Experto en zombis. Especialista en viajes en general. Friki de la televisión”.